Examples

The Quantum Gate Decomposer (QGD) package provides static and shared libraries (located in the directory path/to/qgd/lib(64)) that can be linked againts our own C++ code. (Alternatively, the C functions defined in python_interface.h can be used to link against C code as well.) The header files of the package are located in the directory path/to/qgd/include In the forthcoming sections we provide some tricks and best practices to use the QGD API. Also, the QGD API is supprted by a Doxygen documentation, which can be accessed trough the file path/to/qgd/Docs/html/index.html. (To build the Doxygen documentation follow the manual at Main Page.)

The QGD Python interface can be tested by running the decomposition_test executable in the directory path/to/qgd/bin. (To install the QGD package follow the manual at Main Page).

The expected outcome of the test script should look as:

Expected result for the 4th IBM Challenge problem

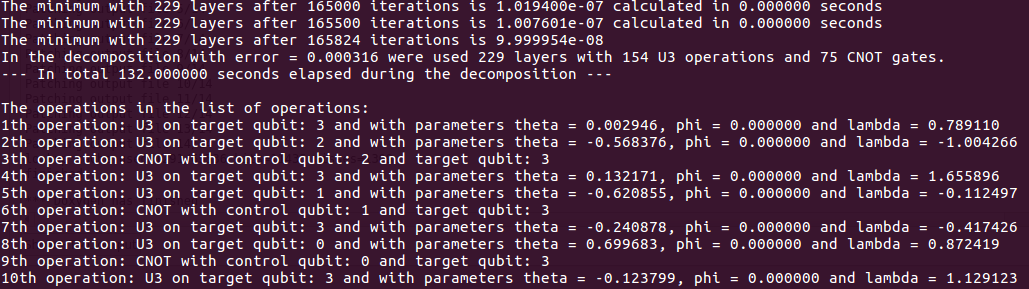
The output informs us that the 4-qubit unitary was decomposed by using 75 CNOT gates with decomposition error 0.000316. These information are followed by the list of the decomposing operations.

Using the QGD library

In this example we show how to use the QGD library for developing applications using the decomposition capabilities of the QGD package. Here we explain the steps provided in the example file decomposition_test.cpp to decompose a general random 4-qubit unitary.

To include the functionalities of the QGD package, provide the following lines in your code:

#include "qgd/common.h"
#include "qgd/N_Qubit_Decomposition.h"
#include "qgd/Random_Unitary.h"

The first include provide basic functionalities of the QGD package, for example methods for aligned memory allocation and memory release. The second line includes the definition of the class to perform the decomposition of the N-qubit unitaries. This class is the key element to access the decomposition capabilities of the QGD package. The third line imports the method and class definitions for creating random unitaries to be decomposed.

The QGD package provides two ways to create random unitaries. The first way can be used to construct a random unitary as a product of CNOT and U3 operations. The parameters of the operations are chosen randomly, but the overall number of CNOT operations is predefined:

    // The number of qubits spanning the random unitary
    int qbit_num = 4;

    // the number of rows of the random unitary
    int matrix_size = Power_of_2(qbit_num);

    // creating random unitary constructing from 6 CNOT gates.
    int cnot_num = 6;
    Matrix Umtx_few_CNOT = few_CNOT_unitary( qbit_num, cnot_num);

The code snippet above demonstrates the way to create a random unitary describing qbit_num qubits and constructed from cnot_num number of CNOT operations. The constructed unitary is returned through the preallocated Umtx_few_CNOT array. The second method can be used to construct general random unitaries based on the parametrization of arXiv:1303:5904v1.

    // creating class to generate general random unitary
    Random_Unitary ru = Random_Unitary(matrix_size);
    // create general random unitary
    Matrix Umtx = ru.Construct_Unitary_Matrix();

After the creation of the unitary to be decomposed we create an instance of class N_Qubit_Decomposition to perform further calculations:

    // creating the class for the decomposition. Here Umtx_adj is the complex transposition of unitary Umtx
    N_Qubit_Decomposition cDecomposition = N_Qubit_Decomposition( Umtx_adj, qbit_num, /* optimize_layer_num= */ false, /* initial_guess= */ RANDOM );

Notice, that we gave the complex transpose of the unitary Umtx as an input for the class N_Qubit_Decomposition. This can be explained by simple linear algebra considerations: since the product of the unitary with it's complex transpose ( 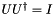) gives identity, the sequence of operations bringing a unitary 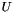into identity would naturally equal to the complex transpose 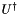of the unitary .

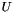Along with the input unitary we provided two other inputs for the decomposition class.

• optimize_layer_num Set true to try to find the fewest number of CNOT gates necessary for the decomposition (increasing the running time) or false when the predefined maximal number of layer gates is used for the decomposition (which fit better for general unitaries).
• initial_guess String indicating the method to guess initial values for the optimization. Possible values:
  • ZEROS: the initial guessed values are all zeros,
  • RANDOM: the initial guessed values are random doubles,
  • CLOSE_TO_ZERO: the initial guessed values are random numbers close to zero.

In case we would like to try to minimize the number of CNOT gates in the decomposition, the best choice for the initial_guess values are ZEROS (discussed in more details in the forthcoming sections). However, this kind of the choice might result unwanted convergence of the optimization to local minimum instead of the global one. Thus, the solution of this example might sometimes fail to reach the global minimum. For the same reason, unitaries consisting of much CNOT gates can be well decomposed by initial guess values RANDOM or CLOSE_TO_ZERO.

Finally, before we start the decomposition, we set some other parameters for the decomposition:

    // setting the number of successive identical layers used in the decomposition
    std::map<int,int> identical_blocks;
    identical_blocks[3] = 1;
    identical_blocks[4] = 2;
    cDecomposition.set_identical_blocks( identical_blocks );

    // setting the maximal number of layers used in the decomposition
    std::map<int,int> num_of_layers;
    num_of_layers[2] = 3;
    num_of_layers[3] = 16;
    num_of_layers[4] = 60;
    num_of_layers[5] = 240;
    num_of_layers[6] = 960;
    num_of_layers[7] = 3775;
    cDecomposition.set_max_layer_num( num_of_layers );

    // setting the number of optimization iteration loops in each step of the decomposition
    std::map<int,int> num_of_iterations;
    num_of_iterations[2] = 3;
    num_of_iterations[3] = 1;
    num_of_iterations[4] = 1;
    cDecomposition.set_iteration_loops( num_of_iterations );

    // setting operation layer
    cDecomposition.set_optimization_blocks( 1 );

    // setting the verbosity of the decomposition
    cDecomposition.set_verbose( true );

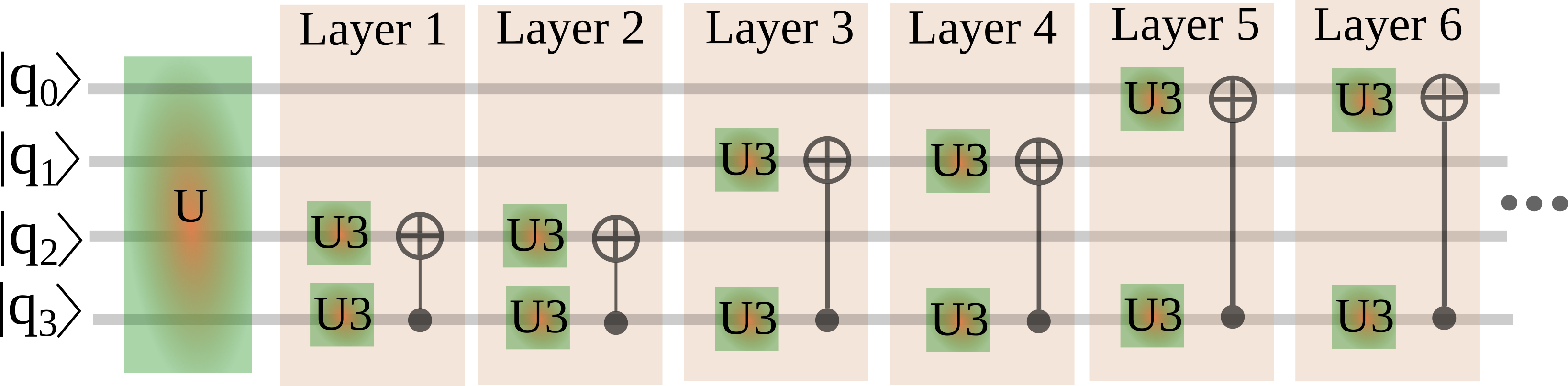
By setting the number of identical blocks in the code snippet we order the code to use two identical successive blocks for the sub-disentanglement of the 4-qubit unitary:

Two identical successive block in the sub-decomposition of the 4th qubit

and do not use repeated successive blocks in the decomposition of the 3-qubit submatrix:

No repeated successive blocks in the sub-decomposition of the 3rd qubit

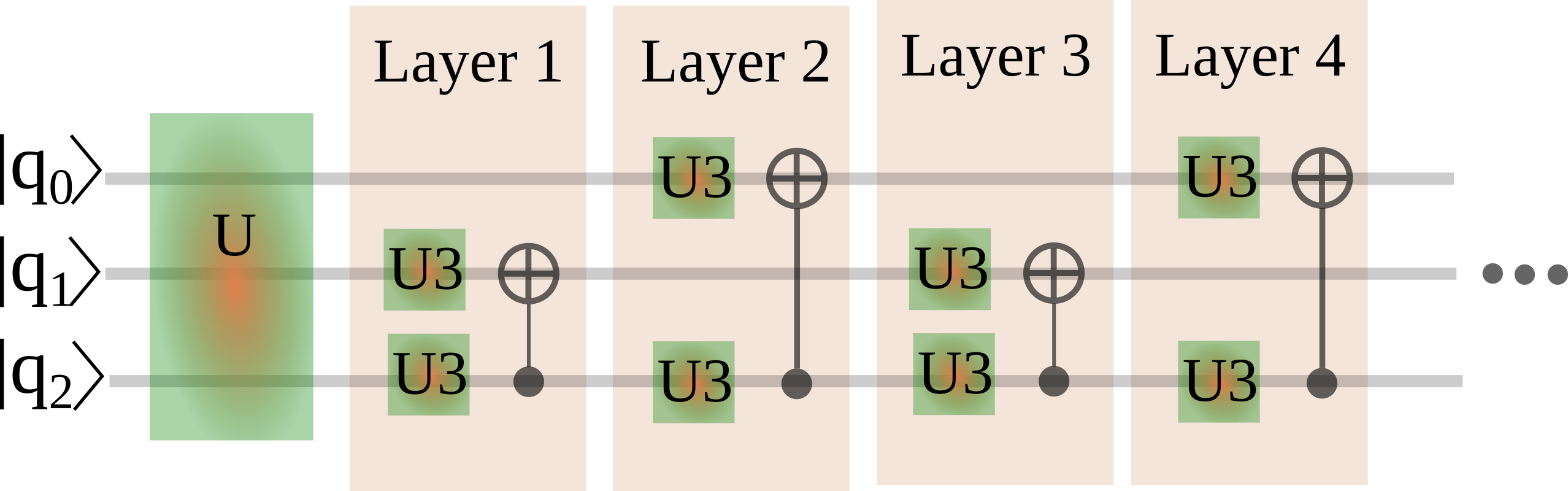
The idea behind setting two identical successive block is very straightforward. In this case the successive CNOT gates might cancel each other resulting in possible simplification of the gate structure in the end of the decomposition process. Notice, that setting more the three identical blocks has no sense, since all two-qubit unitaries can be decomposed with at most three CNOT gates.

In the second part of the code snippet above we set the maximal number of operation blocks allowed in the n-qubit sub-decomposition problem. The demonstrated choices correspond to the number of layers needed to the decomposition of general N-qubit unitaries. (These maximal parameters are in-built in the code, it is not necessary to provide them in the code.) In more specific problems the unitary might be decomposed by fewer CNOT gates. In such cases we can define the upper bond of the decomposition operation blocks via these settings.

The third part in the above code snippet is about the setting of the number of iterations in each optimization step used during the sub-decomposition of the n-th qubit. By default, the number of iteration loops are set to one, however in case of specific unitaries, it is advised to increase the number of iteration loops to avoid unwanted convergence to local minima. (On the other hand, the increase of the iteration loops might increase the running time.) We notice, that the best choice of the above parameters varies from problem to problem. One should give a try to multiple set of parameters to find the best decomposition of the unitary.

In the last command of the code snippet above one can set the verbosity of the decomposition to on/off by the value True/False. After setting the parameters of the decomposition we can start the optimization process by the command:

    // starting the decomposition
    cDecomposition.start_decomposition(/* finalize_decomposition = */ true, /* prepare_export= */ true);

    cDecomposition.list_operations(1);

The last command in the above code snippet prints the decomposing operations into the standard output. For further programming usage the list of decomposed operations can be retrieved via the method N_Qubit_Decomposition.get_operations of the class N_Qubit_Decomposition.

Compiling and linking against QGD libraries

To successfully compile a software using the QGD package, one need to provide the include path of the header files for the compiler. This can be done by providing the compiler flag -Ipath/to/qgd/include at compilation time. After a successful installation described at Main Page the header files are copied in to the include directory in the QGD installation location.

Similarly, the QGD libraries are installed into the directory path/to/qgd/lib(64). In order to link against the installed libraries located in path/to/qgd/lib(64), you must either use libtool, and specify the full pathname of the library, or use the -Lpath/to/qgd/lib(64) flag during linking and do at least one of the following:

• add path/to/qgd/lib(64) to the 'LD_LIBRARY_PATH' environment variable during execution
• add path/to/qgd/lib(64) to the 'LD_RUN_PATH' environment variable during linking
• use the '-Wl,-rpath -Wl,path/to/qgd/lib(64)' linker flag
• have your system administrator add path/to/qgd/lib(64) to '/etc/ld.so.conf'

Another option to build portable standalone application is to link against static library of the QGD named libqgd.a located in the directory path/to/qgd/lib(64).