Introduction

The Quantum Gate Decomposer (QGD) package provides a very simple interface to Python which makes it possible to combine QGD with well known quantum computing back ends, like Qiskit. In fact, QGD has already established an interface to export the decomposed quantum circuit in Qiskit format. The Python interface of QGD is developed using Ctypes, while all the massive calculations related to the decomposition run in native C, and only the input and final output parameters are casted between C and Python types.

In the forthcoming sections we provide some tricks and best practices to use the QGD Python interface. The QGD Python interface can be tested by running the example.py script right in the installation directory of the QGD package: (To install the QGD package follow the manual at Main Page. If the QGD package was compiled with OpenMP than one can also externally set the number of logical threads by the environment variable OMP_NUM_THREADS.)

$ cd path/to/qgd && python3 example.py

The example solves two problems:

the decomposition of a general three-qubit unitary
the decomposition of the 4th IBM Challenge problem

The expected outcome of the test script should look as:

Expected result for the 4th IBM Challenge problem

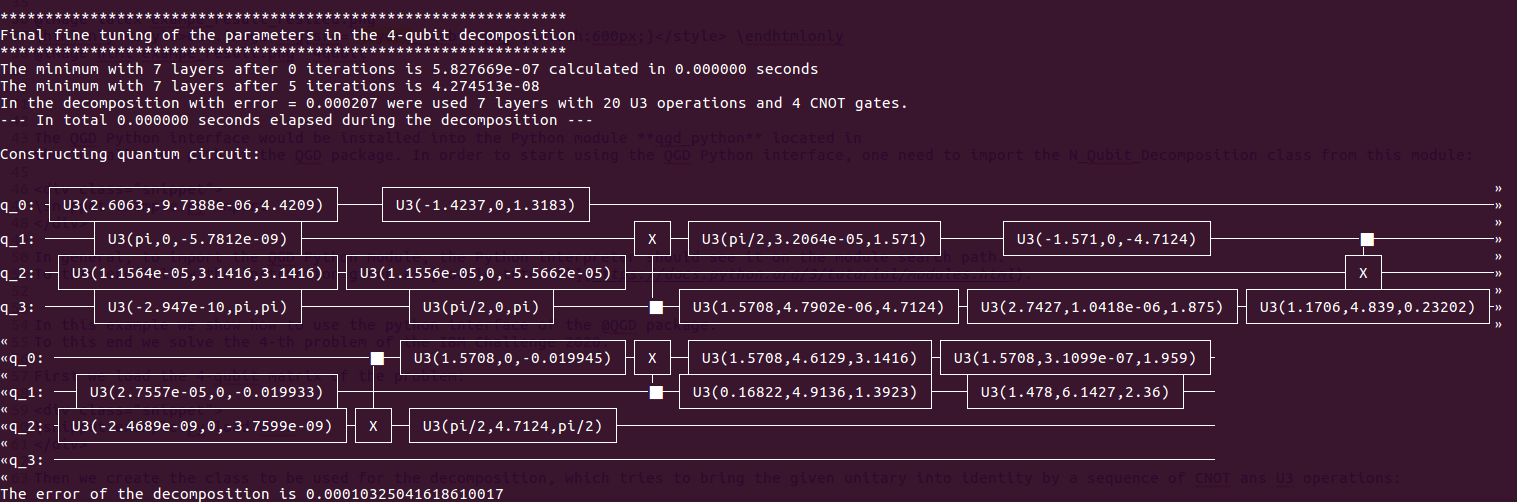
The output informs us that the 4th IBM Challenge problem was solved by using 4 CNOT gates with decomposition error 0.00010325.... It is evident that the given decomposition can be further simplified by the union of successive U3 operations, however the QGD package is not equipped yet to do such simplifications. (The decomposition result of the general three-qubit matrix can be found somewhere above the result of the IBM challenge in the standard output.)

Writing your own scripts

In this example we show how to use the python interface of the Quantum Gate Decomposer package for our own purposes. To this end we demonstrate the steps in the example.py to solve the 4th problem of the IBM Challenge 2020. The QGD Python interface is installed into the Python module qgd_python located in the installation path of the QGD package. In order to start using the QGD Python interface, one need to import the N_Qubit_Decomposition class from this module:

from qgd_python.N_Qubit_Decomposition import N_Qubit_Decomposition

In general, to import the QGD Python module, the Python interpreter should see it on the module search path (for further details see the module tutorial). After loading the qgd_python module we need to load the 4-qubit matrix of the problem from a file shipped with the QGD package:

from scipy.io import loadmat
    
data = loadmat('Umtx.mat')  
Umtx = data['Umtx']

Then we create the class to be used for the decomposition, which tries to bring the given unitary into identity by a sequence of CNOT ans U3 operations:

cDecompose = N_Qubit_Decomposition( Umtx.conj().T, optimize_layer_num=True, initial_guess="zeros" )

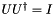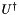Notice, that we gave the complex transpose of the unitary Umtx as an input for the class N_Qubit_Decomposition. This can be explained by simple linear algebra considerations: since the product of the unitary with it's complex transpose ( $U U^\dagger=I$ ) gives identity, the sequence of operations bringing a unitary $U$ into identity would naturally equal to the complex transpose $U^\dagger$ of the unitary $U$ .

Along with the input unitary we provided two other inputs for the decomposition class.

optimize_layer_num Set true to try to find the fewest number of CNOT gates necessary for the decomposition (increasing the running time) or false when the predefined maximal number of layer gates is used for the decomposition (which fit better for general unitaries).
initial_guess String indicating the method to guess initial values for the optimization. Possible values:
- "zeros": the initial guessed values are all zeros,
- "random": the initial guessed values are random doubles,
- "close_to_zero": the initial guessed values are random numbers close to zero.

In case we would like to minimize the number of CNOT gates in the decomposition, the best choice for the initial_guess values are "zeros" (discussed in more details in the forthcoming sections). However, this kind of the choice might result unwanted convergence of the optimization to local minimum instead of the global one. Thus, the solution of this example might sometimes fail to reach the global minimum. For the same reason, unitaries consisting of much CNOT gates can be well decomposed by initial guess values "random" or "close_to_zero".

Finally, before we start the decomposition, we set some other parameters for the decomposition:

# set the number of successive identical blocks in the optimalization of disentanglement of the n-th qubits
cDecompose.set_identical_blocks( {4: 2, 3: 1} )
# set the maximal number of layers in the decomposition
cDecompose.set_max_layer_num( {4: 9, 3:4})
# set the number of iteration loops in the decomposition
cDecompose.set_iteration_loops({4: 3, 3: 3, 2: 3})
# setting the verbosity of the decomposition
cDecompose.set_verbose( True )

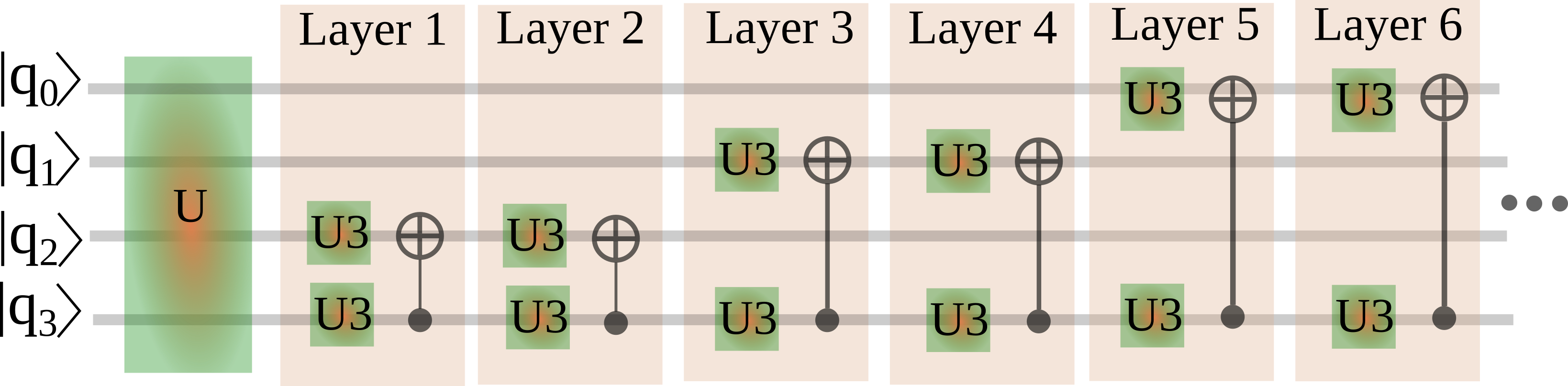
By setting the number of identical blocks in the code snippet we order the code to use two identical successive blocks for the sub-disentanglement of the 4-qubit unitary:

Two identical successive block in the sub-decomposition of the 4th qubit

and do not use repeated successive blocks in the decomposition of the 3-qubit submatrix:

No repeated successive blocks in the sub-decomposition of the 3rd qubit

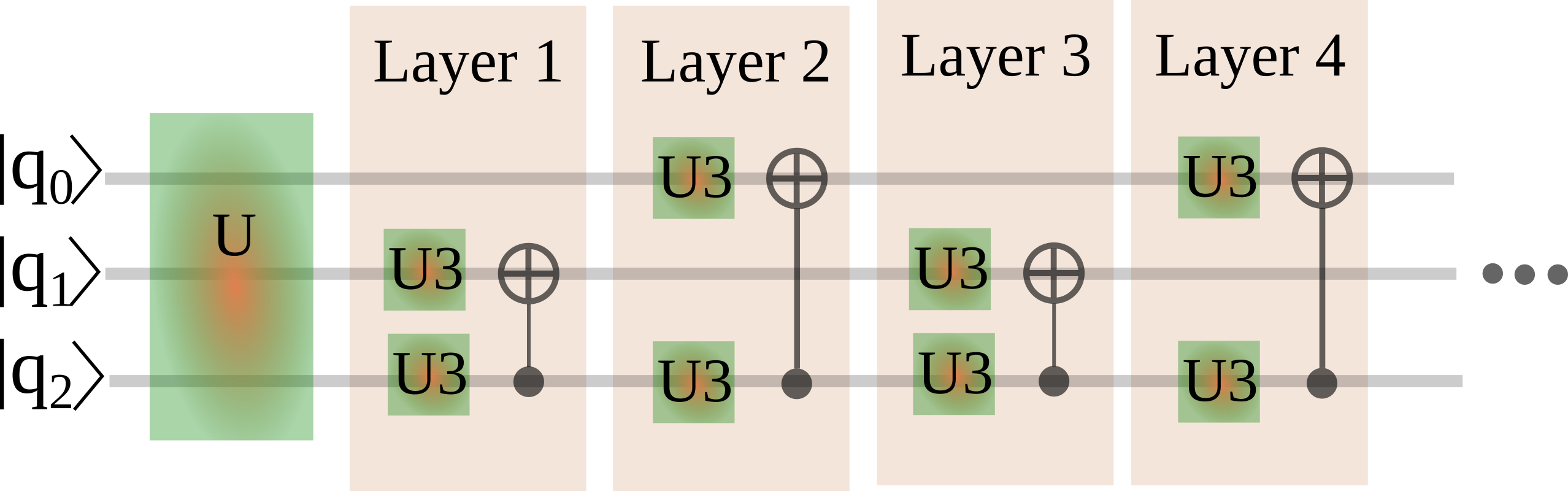
The idea behind setting two identical successive block is very straightforward. In this case the successive CNOT gates might cancel each other resulting in possible simplification of the gate structure in the end of the decomposition process. Notice, that setting more the three identical blocks has no sense, since all two-qubit unitaries can be decomposed with at most three CNOT gates.

In the second command of the code snippet above we set the maximal number of operation blocks allowed in the n-qubit sub-decomposition problem. The demonstrated choices are very much specific for the given problem. In case of general random unitaries, when the unitary is spanned by four qubits, than 60 operation blocks (layers) are needed to solve the sub-disentanglement problem, while for the sub-decomposition of a unitary spanned by three qubits are necessary at most 20 operation blocks. (These maximal parameters are in-built in the code, it is not necessary to provide them in the code.)

The third command in the above code snippet is about the setting of the number of iterations in each optimization step used during the sub-decomposition of the nth qubit. By default, the number of iteration loops are set to one, however in case of specific unitaries, such as the matrix of the 4th problem of the IBM challenge, it is advised to increase the number of iteration loops to avoid unwanted convergence to local minima. (On the other hand, the increase of the iteration loops might increase the running time.) We notice, that the best choice of the above parameters varies from problem to problem. One should give a try to multiple set of parameters to find the best decomposition of the unitary.

In the last command of the code snippet above one can set the verbosity of the decomposition to on/off by the value True/False. After setting the parameters of the decomposition we can start the optimization process by the command:

# starting the decomposition
cDecompose.start_decomposition()
# list the decomposing operations
cDecompose.list_operations()

The second command in the above code snippet prints the list of decomposing operations on the standard output. Finally, we can export a Qiskit compatible quantum circuit via the QGD Python interface and calculate the final error of the decomposition by the following code snippet:

print(' ')
print('Constructing quantum circuit:')
print(' ')
quantum_circuit = cDecompose.get_quantum_circuit()
print(quantum_circuit)
from qiskit import execute
from qiskit import Aer
import numpy.linalg as LA
    
# test the decomposition of the matrix
backend = Aer.get_backend('unitary_simulator')
    
job = execute(quantum_circuit, backend)
result = job.result()
    
decomposed_matrix = result.get_unitary(quantum_circuit)
    
product_matrix = np.dot(Umtx, decomposed_matrix.conj().T)
decomposition_error =  LA.norm(product_matrix - np.identity(16)*product_matrix[0,0], 2)
print('The error of the decomposition is ' + str(decomposition_error))

The documentation of Qiskit, which is needed to fully understand the above code snippet, can be found here.